You can play with the model and face editions in Colab, or check more about the code in the GitHub repo.

1. Introduction

This article shows a quick overview of a recent project that I developed working on my master’s about how to edit attributes from faces using Variational Autoencoder (VAE)[1][5].

In a practical view, VAE architecture is similar to a vanilla Autoencoder. However, at the Neural Network bottleneck, their neurons learn a Multivariate Gaussian distribution such their outcomes represent means and variances of the distribution.

This Multivariate Gaussian distribution is called a latent distribution $Z$, which means they are variables that cannot be observed directly. Thus the distribution of the latent variables is approximated using a Variational Bayesian (VB) approach, also called Variational Inference. As a matter o fact, what is approximated is the posterior distribution $p(Z|X)$. The prior distribution $Z$ is assumed to be a normal $N(0, 1)$.

For more information about VAE and its objective goal, check it out the next post.

To realize this experiment. I used the celebA[2] dataset, which contains around 200 thousand images labeled with 40 binary attributes.

2. The Solution

2.1 The Architecture

The proposed architecture has an additional decoder branch that predicts face masks. During training, the labels of the face masks are used too, which replaces the background of the reconstructed image such that the loss function is applied only over the face pixels. On the other hand, in the prediction mode, the background replacement is done by the predicted mask itself, not requiring any extra input but a sample image.

On training

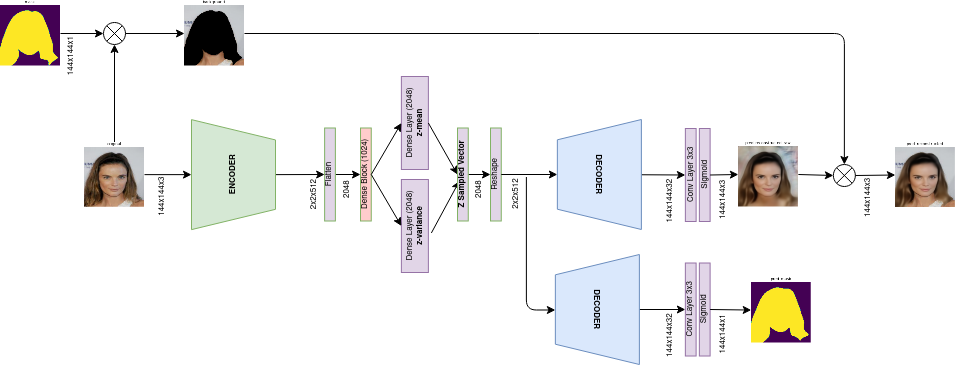
On prediction

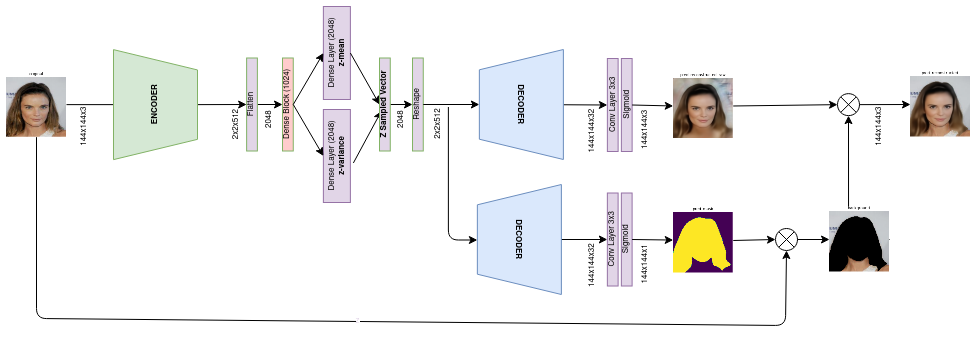
This is, in fact, a deep model containing 145 layers and 16.6M parameters.

2.2 Objective function

The objective function is broken into three parts:

1. Reconstruction of the image: I used the SSIM (Structural Similarity Index), a perceptual loss, and MAE (Mean Absolute Error). SSIM helps the perceptual quality like contrast and helps to avoid the usual blur from L1 and L2 losses. MAE helps to keep the original colors from the images.
2. Prediction of the face mask: I used the Binary Crossentropy and Dice loss for this.
3. Kullback-Leibler divergence: This is a specific loss function that comes from the variational inference approach, which minimizes the divergence and allows us to maximize the Evidence Lower Bound (ELBO) of the VB equation [3]. This divergence measures the dissimilarity between the approximated posterior $q_\phi(z|x)$ and the prior $p(z)$ distribution. As we assume the prior are multivariate normals, we want to make the posterior distributions as normal as possible; therefore, it also acts as a regularizer term.

To not overextend this article, code implementation can be directly seen on the training.py script.

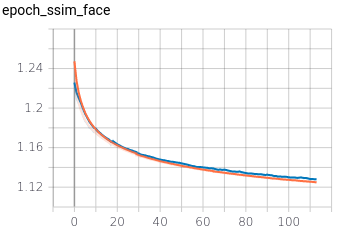
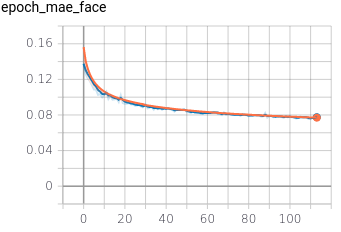
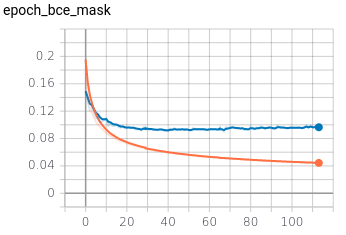
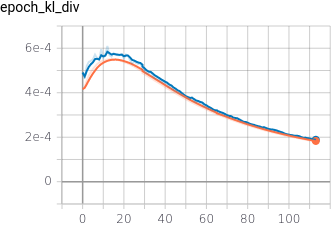
2.3 Training metrics

The training ran for 50 hours on Colab Pro. It did 113 iterations of 4000 steps and a batch size of 32. The training metrics can be seen below.

SSIM and MAE decreased along the training and not suffering variance. The losses (BCE + Dice) on the mask show variance. Although the generalizing capacity looked visually good, the variance seems to be caused by slight gaps in the ground truth mask between the face, ears, and hair.

The KL divergence curve had an odd behavior, initially increasing on the first fifteen iterations and then decreasing afterward. That happened because I scaled the KL divergence factor to $1e-3$ such its regularization effect doesn’t inhibit the reconstruction learning at the beginning of the training; however, it doesn’t avoid the divergence either. After the reconstruction loss is low enough, the NN also starts to “learn” the KL divergence.

2.4 Results

As the main purpose of this architecture is to reconstruct the image, let’s see how it performs:

It does well, although some high-frequency details are lost on the skin and the hair. Make them look polished.

3. Editing Attributes

One of the VAE advantages is its continuous latent space which makes it easy to interpolate vectors on the latent space, allowing us to edit attributes, or even to generate artificial images from random sampling on the latent space $Z$.

3.1 Attribute Spectrum

As it was seen on [4], you can use simple arithmetic to create an attribute vector and edit a sample. I took 10k positive and negative examples for each attribute to compute an attribute vector. Afterward, this vector can be added to the latent sample features. The vector values can be scaled in any factor or direction, expressing different attribute levels.

3.2 Beards

Another example is adding beards of different colors. For that, I created a vector joining the beard presence and the hair color. It is interesting to notice different correlated attributes that follow each color.

I used the same vector scale for all colors, but you can see that some beards were shallow as the blond one, and others were long as the black one. Besides, you have some slight changes in skin colors; for instance, the black beard got a darker skin tone.

3.3 More Attributes

In this example, I like to notice how the edition doesn’t affect “much” the pose and expression of the faces. On the second row, the smiling expression kept practically the same across different editions. Besides, the eyeglasses of all three fitted on the correct position of the face, regarding the top of the nose and the head pose.

4. Conclusions

We just checked that it is possible to synthetically edit generic attributes on a face using VAE, preserving the head pose and facial expressions. However, it does have losses when reconstructing the skin and hair nuances of the original photos, making them smooth on everyone.

References

[1] Diederik P Kingma and Max Welling. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.

[2] Ziwei Liu, Ping Luo, Xiaogang Wang, and Xiaoou Tang. Large-scale celeb faces attributes (celebA) dataset. Retrieved August, 15(2018):11, 2018.

[3] Pattern Recognition and Machine Learning, by Cristopher M. Bishop, Springer-Verlag New York, 2006, pp. 463–463.

[4] Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised representation learning with deep convolutional generative adversarial networks, 2016.

[5] Rezende, D. J., Mohamed, S., & Wierstra, D. (2014, June). Stochastic backpropagation and approximate inference in deep generative models. In International conference on machine learning (pp. 1278-1286). PMLR.